Geometri Dan Rauang

Geometri, berasal dari bahasa Yunani, geo artinya bumi dan metria artinya pengukuran. Sehingga secara harfiah, geometri berarti ilmu pengukuran bumi. Pengertian tersebut muncul, karena pada awal penemuannya, geometri sebagian besar dimulai dari masalah praktis berupa pengukuran segala sesuatu yang ada di bumi untuk keperluan pertanian pada jaman itu (Babylonia dan Mesir Kuno).

Pada perkembangan selanjutnya, geometri tidak hanya menyangkut pengukuran dan sifat keruangan bumi, tetapi berkembang pada obyek-obyek yang bersifat abstrak, seperti titik, ruas garis, garis, segi banyak, bidang banyak dan lain-lain.

1. Segi Banyak (Poligon)

a. Segitiga

Segitiga adalah gabungan ketiga ruas garis hubung dua-dua titik dari tiga titik yang tidak segaris. Berdasarkan konsep tersebut, jelas bahwa segitiga hanya berupa gabungan tiga ruas garis, yang berarti hanya berupa titik-titik pada batas (keliling) saja dan tidak termasuk daerah dalamnya. Segitiga beserta daerah dalamnya disebut daerah segitiga. Oleh karena itu, segitiga tidak mempunyai luas, yang dipunyai segitiga hanyalah panjang (keliling) saja. Sedangkan luas dimiliki oleh daerah segitiga.

Gambar (a) menunjukkan segitiga ABC, sedangkan Gambar (b) menunjukkan daerah segitiga ABC. Teorema berikut memberikan kriteria kapan gabungan tiga ruas garis membentuk segitiga dan kapan tidak.

Teorema 1. (Ketidaksamaan Segitiga) Jumlah panjang sebarang dua sisi sebuah segitiga lebih besar daripada panjang sisi yang ketiga.

Sebagai contoh, diberikan tiga buah ruas garis masing-masing berukuran 4 cm, 7 cm, dan 5 cm. Ketiga ruas tersebut apabila digabung-gabung dapat membentuk sebuah segitiga. Sedangkan, tiga buah ruas garis masing-masing berukuran 4 cm, 7 cm, dan 2 cm, jika digabung-gabung tidak mungkin akan membentuk sebuah segitiga. Sebab 4 + 2 tidak lebih dari 7, seperti disyaratkan Teorema 1.

Teorema 2. Jumlah ukuran sudut-sudut dalam segitiga adalah.

Teorema 3 (Teorema Pythagoras) Dalam segitiga siku-siku, kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kedua sisi siku-sikunya.

Jika dalam sebuah segitiga siku-siku, a dan b masing-masing menyatakan panjang sisi siku-sikunya dan c menyatakan panjang sisi miringnya, maka berlaku

c² = a²+ b²

Contoh 1

Diketahui segitiga ABC dengan panjang sisi-sisinya AB = 18 cm, BC = 15 cm dan AC = 12 cm. Tentukan tinggi segitiga dari titik C ke sisi  AB.

Pembahasan:

Perhatikan Gambar  tersebut di atas, berdasarkan Teorema Pythagoras pada DADC berlaku hubungan t² = 12² – p², dan pada DDBC berlaku hubungan t² = 15 – (18 – p)². Berdasarkan kedua persamaan tersebut diperoleh: 12– p = 15²– (18 – p)²  Û 144 – p² = 225 – (324 – 36p + p²)     Û 144 – p² = 225 – 324 + 36p – p²     Û 144 = –99 + 36p     Û 243 = 36p Û p = 6,75 Selanjutnya p disubstitusikan ke t² = 12² – p² diperoleh: t² = 12² – p² = 144 – 6,75² = 144 – 45,5625 = 98,4375. Sehingga diperoleh  t = √98,4375  = 9,92. Jadi tinggi segitiga dari titik C ke sisi  AB  adalah 9,92 cm.

2. Segiempat Segi empat adalah gabungan empat ruas garis yang menghubungkan empat titik, dengan tiga-tiga titik tidak segaris, dan mempunyai sifat-sifat :

• Tidak ada ruas garis yang berpotongan, kecuali di titik-titik ujungnya.
• Setiap titik merupakan titik ujung tepat dari dua ruas garis.

Jenis-jenis segiempat yaitu jajar genjang, belah ketupat, persegi panjang, persegi (bujur sangkar), trapesium dan layang-layang. 1). Jajar Genjang Jajar genjang adalah segiempat dengan sifat kedua pasang sisi berhadapan saling sejajar.  Berdasarkan pengertian jajar genjang, dapat diturunkan sifat –sifat jajar genjang seperti dinyatakan dalam teorema berikut.

Teorema 4 a). Dalam sebuah jajar genjang, sisi-sisi yang berhadapan kongruen (sama panjang);b). Dalam sebuah jajar genjang, sudut-sudut yang berhadapan kongruen (sama besar);c). Dalam sebuah jajar genjang, diagonal-diagonalnya berpotongan di tengah-tengah.

Tidak semua segiempat berbentuk jajar genjang. Bagaiman ciri-ciri (kriteria) segiempat yang merupakan jajar genjang dinyatakan dalam teorema berikut.

Teorema 5 a). Suatu segiempat disebut jajar genjang, jika sisi-sisi yang berhadapan kongruen;b). Suatu segiempat disebut jajar genjang, jika sudut-sudut yang berhadapan kongruen;c). Suatu segiempat disebut jajar genjang, jika diagonal-diagonalnya berpotongan di tengah-tengah;

2). Belah Ketupat Belah ketupat adalah jajar genjang dengan sifat dua sisi yang berturutan kongruen (sama panjang) atau belah ketupat adalah segiempat dengan sifat kedua pasang sisi berhadapan saling sejajar, dan dua sisi yang berturutan kongruen (sama panjang). Berdasarkan pengertiannya jelas bahwa belah ketupat merupakan jajar genjang, tetapi tidak sebalinya.  Oleh karena itu sifat-sifat yang berlaku pada jajar genjang juga berlaku pada belah ketupat.  Berdasarkan pengertian belah ketupat diperoleh sifat –sifat belah ketupat yang selengkapnya dinyatakan dalam teorema berikut. Teorema 6

• Dalam sebuah belah ketupat, keempat sisi-sisinya kongruen;
• Dalam sebuah belah ketupat, sudut-sudut yang berhadapan kongruen;
• Dalam sebuah belah ketupat, diagonal-diagonalnya berpotongan di tengah-tengah;
• Dalam sebuah belah ketupat, diagonal-diagonalnya membagi sudut-sudut menjadi dua bagian yang kongruen;
• Dalam sebuah belah ketupat, diagonal-diagonalnya berpotongan tegak lurus satu dengan yang lain;

Bagaiman ciri-ciri (kriteria) segiempat yang merupakan belah ketupat dinyatakan dalam teorema berikut. Teorema 7

• Jika dalam suatu jajar genjang diagonal-diagonalnya membagi sudut-sudut menjadi dua bagian yang kongruen, maka jajar genjang tersebut adalah belah ketupat.
• Jika dalam suatu jajar genjang diagonal-diagonalnya berpotongan tegak lurus satu dengan yang lain, maka jajar genjang tersebut adalah belah ketupat.

3). Persegi Panjang Persegi panjang adalah jajar genjang yang salah satu sudutnya siku-siku, yang ekuivalen dengan persegi panjang adalah segiempat dengan sifat kedua pasang sisi berhadapan saling sejajar dan salah satu sudutnya siku-siku.  Berdasarkan pengertian persegi panjang diperoleh sifat –sifat persegi panjang yang selengkapnya dinyatakan dalam teorema berikut. Teorema 8

• Dalam sebuah persegi panjang, keempat sudutnya siku-siku.
• Dalam sebuah persegi panjang, sisi-sisi yang berhadapan kongruen.
• Dalam sebuah persegi panjang, diagonal-diagonalnya berpotongan di tengah-tengah.
• Dalam sebuah persegi panjang, diagonal-diagonalnya sama panjang.

Bagaiman ciri-ciri (kriteria) segiempat yang merupakan persegi panjang dinyatakan dalam teorema berikut. Teorema 9 Jika dalam suatu segiempat sisi-sisi berhadapannya sejajar dan diagonal-diagonalnya sama panjang, maka segiempat tersebut adalah persegi panjang. 4). Persegi Persegi adalah persegi panjang yang dua sisi berturutannya sama panjang, yang ekuivalen dengan persegi adalah segiempat dengan sifat kedua pasang sisi berhadapan saling sejajar, salah satu sudutnya siku-siku dan dua sisi yang berturutan sama panjang. Berdasarkan pengertian persegi diperoleh sifat –sifat persegi yang selengkapnya dinyatakan dalam teorema berikut. Teorema 10

• Dalam sebuah persegi, keempat sisinya kongruen.
• Dalam sebuah persegi, keempat sudut siku-siku.
• Dalam sebuah persegi, diagonal-diagonalnya berpotongan di tengah-tengah.
• Dalam sebuah persegi, diagonal-diagonalnya sama panjang.
• Dalam sebuah persegi, diagonal-diagonalnya tegak lurus sesamanya.
• Dalam sebuah persegi, diagonal-diagonalnya membagi sudut-sudut menjadi dua bagian yang kongruen, dan masing-masing berukuran 45°.

5). Trapesium Trapesium adalah segi empat yang tepat sepasang sisi berhadapan saling sejajar, sedangkan pasangan sisi yang lain tidak sejajar. Berdasarkan pengertian tersebut jelas bahwa jajargenjang bukanlah kejadian khusus dari trapesium.  Dalam suatu trapesium, sisi-sisi yang sejajar disebut sisi-sisi alas. Sedangkan sisi-sisi yang tidak sejajar disebut kaki-kaki trapesium. Trapesium tidak mempunyai sifat khusus. Jenis-jenis trapesium yaitu 1) trapesium sama kaki, yaitu trapesium yang kedua kakinya sama panjang, 2) trapesium siku-siku, yaitu trapesium yang salah satu sudutnya siku-siku, dan 3) trapesium sebarang, yaitu trapesium yang keempat sisi-sisinya tidak ada yang sama panjang. Teorema 11

• Dalam trapesium sama kaki, sudut-sudut alasnya kongruen.
• Dalam trapesium sama kaki, diagonal-diagonalnya kongruen.

Sedangkan layang-layang adalah segiempat yang sepasang sisi berdekatan kongruen dan sepasang sisi berdekatan lain yang sisi-sisinya berbeda dengan sisi-sisi pada pasangan pertama juga kongruen. Sifat –sifat layang-layang yaitu:

• Diagonal-diagonalnya berpotongan tegak lurus.
• Salah satu diagonalnya dipotong menjadi dua bagian sama panjang oleh diagonal yang lain.

2. Luas Daerah Segi Banyak a. Pengukuran Luas Daerah 1) Daerah Segi-n dan Luas Satuan Banyak orang yang tidak dapat membedakan antara segi-n dan daerah segi-n, padahal kedua istilah itu menyatakan konsep yang berbeda. Daerah segi–n adalah himpunan titik-titik pada segi–n beserta titik-titik di daerah dalamnya. Untuk membedakan, segi–n dan daerah segi–n, diberikan contoh persegi panjang dan daerah persegi panjang sebagai berikut.

Gambar (a). menyatakan persegi panjang sedangkan Gambar (b). menyatakan daerah persegi panjang. Perlu diperhatikan bahwa persegi panjang tidak mempunyai ukuran luas, ukuran yang dimiliki persegi panjang adalah panjang persegi panjang, yang disebut keliling persegi panjang, Sedangkan daerah persegi panjang, ukuran yang dimiliki adalah luas. Mengukur luas suatu daerah berarti membandingkan besar suatu daerah dengan daerah lain yang digunakan sebagai patokan. Luas daerah yang digunakan sebagai patokan ada yang standar dan ada yang tidak standar. Luas daerah yang digunakan sebagai patokan disebut sebagai luas satuan. Luas satuan adalah luas daerah persegi yang panjang sisi-sisinya satu satuan panjang.

b. Luas Daerah Persegi Panjang Luas daerah persegi panjang adalah banyaknya luas satuan yang dapat dimasukkan ke dalam daerah persegi panjang tersebut. Berdasarkan pengertian tersebut dapat disusun Teorema berikut. Teorema 12 Luas daerah persegi panjang sama dengan hasil kali panjang alas dengan tinggi persegi panjang tersebut. Jika luas daerah persegi panjang dinyatakan dengan L (satuan luas), panjang alas dengan p (satuan panjang) dan lebarnya dengan l (satuan panjang), maka

 L = p x l.

Contoh 2 Sebuah plat baja berbentuk persegi panjang dipanaskan sehingga mengalami pemuaian. Jika pertambahan muai panjang dan lebarnya masing-masing 5% dari ukuran semula, tentukan persentase pertambahan luas plat baja tersebut terhadap luas mula-mula. Pembahasan: Misal panjang pesegi panjang mula-mula p (satuan panjang) dan lebar t (satuan panjang). Panjang persegi panjang setelah dipanaskan = p + 2 x 0,05 p = 1,1 p, sedangkan lebar persegi panjang setelah dipanaskan = t + 2 x 0,05 t = 1,1 t.  Luas plat baja mula-mula =  p x t = pt (satuan luas). Luas plat baja setelah dipanaskan =  1,1 p x 1,1 t = 1,21 pt (satuan luas). Pertambahan luas = 1,21 pt – pt = 0,21 pt (satuan luas). Persentase pertambahan luas plat baja =   0,21 pt/pt x  100% =  21 %.

c. Luas Daerah Persegi

Luas daerah persegi adalah banyaknya luas satuan yang dapat dimasukkan ke dalam daerah persegi tersebut. Berdasarkan luas daerah persegi panjang diturunkan luas daerah persegi seperti dinyatakan dalam Teorema berikut.

Teorema 13

Luas daerah persegi sama dengan kuadrat panjang sisi persegi tersebut. Jika luas daerah persegi dinyatakan dengan L (satuan luas), panjang sisi-sisinya dengan s (satuan panjang), maka 

L = s²

d. Luas Daerah Jajar Genjang

Luas daerah jajar genjang adalah banyaknya luas satuan yang dapat dimasukkan ke dalam daerah jajar genjang tersebut. Berdasarkan luas daerah persegi panjang, dapat diturunkan rumus luas daerah jajar genjang seperti dinyatakan dalam Teorema berikut.

Teorema 14

Luas daerah jajar genjang sama dengan hasil kali panjang alas dengan tinggi jajar sebut. Jika luas daerah jajar genjang dinyatakan dengan L (satuan luas), panjang alas dengan p (satuan panjang) dan tingginya dengan t (satuan panjang), maka 

L = p x t

e. Luas Daerah Belah Ketupat

Luas daerah belah ketupat adalah banyaknya luas satuan yang dapat dimasukkan ke dalam daerah belah ketupat tersebut. Rumus luas daerah belah ketupat dapat diturunkan dari rumus luas daerah persegi panjang seperti dinyatakan dalam Teorema berikut.

Teorema 15

Luas daerah belah ketupat sama dengan setengah hasil kali panjang diagonal-diagonal belah ketupat tersebut. Jika luas daerah belah ketupat dinyatakan dengan L (satuan luas), panjang diagonal-diagonalnya dengan   (satuan panjang) dan   (satuan panjang), maka 

L = 1/2 x d₁ x d₂ .

Contoh 3

Luas daerah suatu belah ketupat sama dengan 150 cm². Perbandingan panjang diagonal-diagonalnya adalah 3 : 4, tentukan panjang diagonal-diagonal belah ketupat tersebut.

Pembahasan :

 d₁ x d₂ = 3 : 4 Û 4d₁ = 3 d₂ Û d₁ = ¾ d₂

L =	d1 x d2	Û  150 =	d1 x d2
	2		2

                                         Û d₁ x d₂  = 300                                         Û ¾  d₂ x d₂= 300                                         Û d₂ ²  = 300 x 4/3 =400                                         Û  d₂ = √400 = 20 d₁ = ¾ d₂ = ¾  x 20 = 15 Jadi panjang diagonal-diagonal belah ketupat tersebut adalah 15 cm dan 20 cm. f. Luas Daerah Layang-layang Luas daerah layang-layang adalah banyaknya luas satuan yang dapat dimasukkan ke dalam daerah layang-layang tersebut. Rumus luas daerah layang-layang dapat diturunkan dari rumus luas daerah persegi panjang seperti dinyatakan dalam Teorema berikut. Teorema 16 Luas daerah layang-layang sama dengan setengah hasil kali panjang diagonal-diagonal layang-layang tersebut. Jika luas daerah layang-layang dinyatakan dengan L (satuan luas), panjang diagonal-diagonalnya dengan d₁  (satuan panjang) dan d₂   (satuan panjang), maka 

L =  ½ x d₁ x d₂.

g. Luas Daerah Trapesium Luas daerah trapesium adalah banyaknya luas satuan yang dapat dimasukkan ke dalam daerah trapesium tersebut. Berdasarkan luas daerah persegi panjang, dapat diturunkan rumus luas daerah trapesium seperti dinyatakan dalam Teorema berikut. Teorema 17 Luas daerah trapesium sama dengan setengah hasil kali jumlah panjang sisi sejajar dengan tinggi trapesium tersebut. Jika luas daerah trapesium dinyatakan dengan L (satuan luas), panjang sisi-sisi sejajar masing-masing dengan a (satuan panjang) dan b (satuan panjang) serta tingginya dengan t (satuan panjang), maka 

L =½   (a + b) x t

h. Luas Daerah Segitiga

Luas daerah segitiga adalah banyaknya luas satuan yang dapat dimasukkan ke dalam daerah segitiga tersebut. Berdasarkan luas daerah persegi panjang, dapat diturunkan rumus luas daerah segitiga seperti dinyatakan dalam Teorema berikut.

Teorema 18

Luas daerah segitiga sama dengan setengah hasil kali panjang alas dengan tinggi segitiga tersebut. Jika luas daerah segitiga dinyatakan dengan L (satuan luas), panjang alas dengan a (satuan panjang) dan tingginya dengan t (satuan panjang), maka 

L = ½  x a x t 

Contoh 4

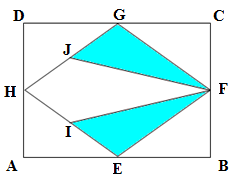
Perhatikan gambar di bawah ini

Diketahui ABCD persegi panjang dengan panjang AB = 24 cm, dan BC = 10 cm. Titik-titik E, F, G dan H secara berturut-turut merupakan titik tengah sisi-sisi AB, BC, CD ada AD, sedangkan I dan J secara berturut-turut merupakan titik tengah ruas garis HE dan HG. Tentukan luas daerah yang diarsir. Pembahasan :

Mudah untuk ditunjukkan bahwa DAEH ≅ DHGD ≅ DGFC ≅ DEBF, akibatnya diperoleh HG = GF = FE = EH. Hal ini berarti bahwa segiempat HEFG merupakan belah ketupat, dengan diagonal-diagonal HF = 24 cm dan EG = 10 cm. 

Karena I dan J masing-masing titik tegah HE dan HG, oleh karena itu diperoleh HI = HJ. Dengan Teorema yang sama, dapat ditunjukkan bahwa DIEF ≅ DJFG, akibatnya diperoleh IF = JF. Dengan hasil ini dapat disimpulkan bahwa segiempat IFJH merupakan suatu layang-layang, dengan diagonal-diagonal HF = 24 cm dan IJ = 5 cm. Luas daerah yang diarsir = Luas daerah belah ketupat HEFG – Luas daerah layang-layang HIFJ. 

HF x EG	-	HF x IJ	=	24 x 10	-	24 x 5
2		2		2		2

                                      = 120 – 60 = 60 Jadi luas daerah yang diarsir = 60 cm². 3. Bidang Banyak dan Daerah Bidang Banyak. Perlu diperhatikan bahwa berdasarkan definisi bidang banyak, yang dimaksud dengan bidang banyak hanyalah permukaannya saja tidak termasuk daerah dalamnya. Bidang banyak beserta daerah dalamnya disebut daerah bidang banyak (bidang banyak pejal atau bidang banyak solid). Bidang banyak tidak mempunyai ukuran volume, ukuran yang dimiliki bidang banyak adalah luas daerah, yang disebut luas permukaan bidang banyak. Sedangkan daerah bidang banyak, disamping mempunyai luas, juga mempunyai volume. Mengukur volume suatu daerah bidang banyak berarti membandingkan besar suatu daerah bidang banyak dengan daerah bidang banyak lain yang digunakan sebagai patokan. Volume daerah bidang banyak yang digunakan sebagai patokan (standar) disebut sebagai volumne satuan. Volume satuan adalah volume daerah kubus yang panjang rusuk-rusuknya satu satuan panjang. a. Volume dan Luas Permukaan Balok Volume  daerah balok, atau disingkat volume balok, adalah banyaknya volume satuan yang dapat dimasukkan ke dalam balok tersebut hingga penuh dan balok tersebut berubah menjadi daerah balok. Berdasarkan pengertian tersebut dapat disusun Teorema berikut.

Teorema 19

Volume balok sama dengan jumlahan dari hasil kali panjang dan lebar, hasil kali panjang dan tinggi, dan hasil kali lebar dan tinggi. Jika volume balok dinyatakan dengan V (satuan volume), panjang balok p (satuan panjang), lebar balok l (satuan panjang) dan tinggi balok t (satuan panjang), maka/span>

V = p x l x t

Luas permukaan balok adalah jumlah seluruh luas daerah sisi-sisi balok. Untuk menentukan luas permukaan balok, akan lebih mudah jika balok dipotong- potong sepanjang rusuk-rusuknya dan dihamparkan pada bidang datar untuk mendapatkan jaring-jaring balok seperti nampak pada gambar di bawah ini.

Berdasarkan gambar di atas, nampak bahwa balok mempunyai enam sisi, yang terdiri dari tiga pasang daerah persegi panjang yang kongruen

Teorema 20

Jika luas permukaan balok dinyatakan dengan L (satuan luas), panjang balok p (satuan panjang), lebar balok l (satuan panjang) dan tinggi balok t (satuan panjang), maka

L = 3(pl + pt + lt)

b. Volume dan Luas Permukaan Kubus

Volume  daerah kubus, atau disingkat volume kubus, adalah banyaknya volume satuan yang dapat dimasukkan ke dalam kubus tersebut hingga penuh dan kubus tersebut berubah menjadi daerah kubus. Berdasarkan pengertian tersebut dapat disusun Teorema berikut.

Teorema 21

Volume kubus sama dengan hasil kali panjang rusuk-rusuknya. Jika volume kubus dinyatakan dengan V (satuan volume), panjang rusuk-rusuknya r (satuan panjang), maka

V = r x r x r = r³

Luas permukaan kubus adalah jumlah seluruh luas daerah sisi-sisi kubus. Untuk menentukan luas permukaan kubus, akan lebih mudah jika kubus dipotong-potong sepanjang rusuk-rusuknya dan dihamparkan pada bidang datar untuk mendapatkan jaring-jaring kubus seperti nampak pada gambar di bawah ini:

Karena kubus mempunyai enam sisi yang berbentuk daerah-daerah persegi kongruen, maka diperoleh rumus sebagai berikut. Teorema 22 Jika luas permukaan kubus dinyatakan dengan L (satuan luas), dan panjang rusuk-rusuknya r (satuan panjang), maka

L = 6 x r x r = 6r²

c. Volume dan Luas Permukaan Prisma

Volume daerah prisma, atau disingkat volume prisma, adalah banyaknya volume satuan yang dapat dimasukkan ke dalam prisma tersebut hingga penuh dan tersebut tersebut berubah menjadi daerah prisma. Prisma banyak jenisnya tergantung bentuk (jenis) alasnya. Pada hakikatnya cara menentukan rumus volume prisma dengan menggunakan pendekatan volume balok atau volume kubus. Volume prisma dinyatakan dengan formula sebagai berikut.

Teorema 23

Volume prisma sama dengan hasil kali luas alas dengan tingginya. Jika volume prisma dinyatakan dengan V (satuan volume), luas alasnya L_a (satuan luas) dan tingginya t (satuan panjang), maka

V = L_a x t

Luas permukaan prisma adalah jumlah seluruh luas daerah sisi-sisi prisma. Untuk menentukan luas permukaan prisma akan lebih mudah jika prisma dipotong-potong sepanjang rusuk-rusuknya dan dihamparkan pada bidang datar untuk mendapatkan jaring-jaring prisma. Jaring-jaring prisma terdiri dari tiga bagian, yaitu dua sisi alas (beberapa literatur menyebut sisi alas dan sisi atas) yang bentuknya berupa daerah segi banyak (poligon) dan sisi samping yang bentuknya berupa daerah persegi panjang. Beberapa jaring-jaring prisma nampak seperti pada gambar  di bawah ini:

Luas permukaan prisma ditentukan dengan rumus sebagai berikut. Teorema 24

Jika luas permukaan prisma dinyatakan dengan L (satuan luas), luas alasnya dengan L _a(satuan luas), keliling alas dengan K (satuan panjang) dan tingginya dengan t (satuan panjang), maka

L = 2L _a+ Kt

d. Volume dan Luas Permukaan Limas

Volume daerah limas, atau disingkat volume limas, adalah banyaknya volume satuan yang dapat dimasukkan ke dalam limas tersebut hingga penuh dan prisma tersebut berubah menjadi daerah limas. Sama seperti prisma, jenis limas tergantung bentuk (jenis) alasnya. Pada hakikatnya cara menentukan rumus volume limas dengan menggunakan pendekatan volume balok atau volume kubus. Volume limas dinyatakan dengan formula sebagai berikut.

Teorema 25

Volume limas sama dengan sepertiga hasil kali luas alas dengan tingginya. Jika volume limas dinyatakan dengan V (satuan volume), luas alasnya La (satuan luas) dan tingginya t (satuan panjang), maka

V = 1/3x L_{a x t}

Luas permukaan limas adalah jumlah seluruh luas daerah sisi-sisi limas. Jenis limas tergantung bentuk (jenis) alasnya, oleh karena itu jaring-jaring limas juga tergantung jenis limasnya Beberapa jaring-jaring prisma nampak seperti pada gambar  di bawah ini:

Teorema 26 Jika Luas permukaan limas ditentukan dengan rumus sebagai berikut.

luas permukaan limas dinyatakan dengan L (satuan luas), luas alasnya dengan L_a(satuan luas), keliling alas dengan K (satuan panjang) dan tinggi segitiga sisi samping dengan (satuan panjang) t_s, maka

L = 2L_a+ ½Kt_s

e. Volume dan Luas Permukaan Tabung

Volume daerah tabung, atau disingkat volume tabung, adalah banyaknya volume satuan yang dapat dimasukkan ke dalam tabung tersebut hingga penuh dan tabung tersebut berubah menjadi daerah tabung. Volume tabung dinyatakan dengan formula sebagai berikut.

Teorema 27

Volume tabung sama dengan hasil kali luas alas dengan tingginya. Jika volume tabung dinyatakan dengan V (satuan volume), jari-jari lingkaran alas r (satuan panjang) dan tingginya t (satuan panjang), maka

V =πr²t

Luas permukaan tabung adalah jumlah seluruh luas daerah sisi-sisi tabung.. Jaring-jaring prisma terdiri dari tiga bagian, yaitu dua sisi alas (beberapa literatur menyebut sisi alas dan sisi atas) yang berbentuk daerah lingkaran dan sisi samping yang berbentuk daerah persegi panjang. Jaring-jaring tabung nampak seperti pada gambar di bawah ini.

Luas permukaan tabung ditentukan dengan rumus sebagai berikut. Teorema 28

Jika luas permukaan tabung dinyatakan dengan L (satuan luas), jari-jari alasnya dengan r (satuan panjang) dan tingginya dengan t (satuan panjang), maka

L = 2πr²+ 2πrt = 2πr(r + t).

f. Volume dan Luas Permukaan Kerucut

Volume  daerah kerucut, atau disingkat volume kerucut, adalah banyaknya volume satuan yang dapat dimasukkan ke dalam kerucut tersebut hingga penuh dan kerucut tersebut berubah menjadi daerah kerucut. Volume kerucut dinyatakan dengan formula sebagai berikut.

Teorema 29

Volume kerucut sama dengan sepertiga hasil kali luas alas dengan tingginya. Jika volume kerucut dinyatakan dengan V (satuan volume), jari-jari lingkaran alas r (satuan panjang) dan tingginya t (satuan panjang), maka

V = 1/3 r²t.

Luas permukaan kerucut adalah jumlah seluruh luas daerah sisi-sisi kerucut. Jaring-jaring kerucut terdiri dari dua bagian, yaitu dua sisi alas yang berbentuk daerah lingkaran dan sisi samping yang berbentuk daerah selimut kerucut. Jaring-jaring kerucut nampak seperti pada gambar di bawah ini. Luas permukaan kerucut ditentukan dengan rumus sebagai berikut:

Teorema 30

Jika luas permukaan kerucut dinyatakan dengan L (satuan luas), jari-jari alasnya dengan r (satuan panjang) dan panjang apotema kerucut dengan t (satuan panjang),

L = pr²+ prs = pr(r + s).

Created By : wasto s.pd | Ngangsu Kawruh

Terimah Kasih telah membaca artikel :Geometri Dan Rauang. Yang ditulis oleh : wasto s.pd .Pada hari : . Jika anda ingin sebarluaskan artikel ini, mohon sertakan sumber link asli. Kritik dan saran dapat anda sampaikan melalui kotak komentar. Trimakasih. Follow@Cahyo Kurmai Setiyawan

<a href="http://cahlumbir.blogspot.com/2014/10/geometri-dan-rauang.html" target="_blank">Geometri Dan Rauang</a>